We have to find the parametric representation of the parabola y = (x+7)² - 5, which is represented in vertex form.
Parametric representations use a third variable on which we define x and y.
We will call this variable t.
We can start with defining t as:
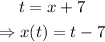
We then have already x in function of t.
Then, we can use the definition of t to find y(t):
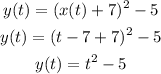
We then have x and y defined in function of t.
Answer: we can represent the parabola in a parametric form as
x(t) = t-7
y(t) = t² - 5