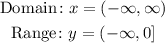Question

Given the graph of a function f. Identify function by name. Then graph the indicated functions. State the domain and the range in set notation.A) f(x-1) -3B) -f(x)

Answer 1

For f(x);

The domain is;

`D\colon x=(-\infty,\infty)`

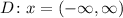
The range is;

`R\colon y=\lbrack0,\infty)`

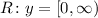
Graphing those points for function A, we have;

The domain and range of the given function A is;

`\begin{gathered} \text{Domain}\colon x=(-\infty,\infty) \\ \text{Range}\colon y=\lbrack-3,\infty) \end{gathered}`

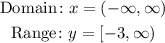
Graphing those points for function B, we have;

The domain and range of the given function B is;

`\begin{gathered} \text{Domain}\colon x=(-\infty,\infty) \\ \text{Range}\colon y=(-\infty,0\rbrack \end{gathered}`

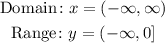
Step-by-step explanation:

Given the function in the attached image;

The function is a square function and can be written as;

`f(x)=x^2`

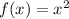
The domain is;

`D\colon x=(-\infty,\infty)`

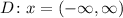
The range is;

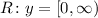
`R\colon y=\lbrack0,\infty)`

A.

`f(x-1)-3=(x-1)^2-3`

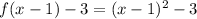
B.

`-f(x)=-x^2`

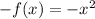
Graphing the functions;

For A;

`\begin{gathered} f(1-1)=(1-1)^2-3=-3 \\ (1,-3) \\ f(3-1)=(3-1)^2-3=1 \\ (3,1) \\ f(-1-1)=(-1-1)^2-3=1 \\ (-1,1) \end{gathered}`

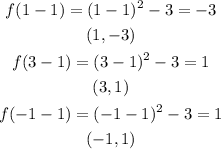
Graphing those points for function A, we have;

The domain and range of the given function A is;

`\begin{gathered} \text{Domain}\colon x=(-\infty,\infty) \\ \text{Range}\colon y=\lbrack-3,\infty) \end{gathered}`

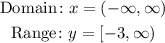
For B;

`\begin{gathered} -f(x)=-x^2 \\ -f(0)=-0^2 \\ (0,0) \\ -f(2)=-2^2=-4 \\ (2,-4) \\ -f(-2)=-(-2)^2=-4 \\ (-2,-4) \end{gathered}`

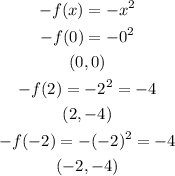
Graphing those points for function B, we have;

The domain and range of the given function B is;

`\begin{gathered} \text{Domain}\colon x=(-\infty,\infty) \\ \text{Range}\colon y=(-\infty,0\rbrack \end{gathered}`