Question

|5-2x|+1≤10 absolute value equations or inequalities and graph the solution set on the number line

Answer 1

The given inequality is

`|5-2x|+1\leq10`

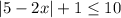
First, we subtract 1 on each side

`\begin{gathered} |5-2x|+1-1\leq10-1 \\ |5-2x|\leq9 \end{gathered}`

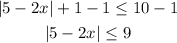
Now we use the property of inequalities with absolute values, which states

`|x|\leq a\rightarrow-a\leq x\leq a`

Using this property, we have

`|5-2x|\leq9\rightarrow-9\leq5-2x\leq9`

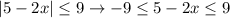
We solve the compound inequality now

`\begin{gathered} -9\leq5-2x\leq9 \\ -9-5\leq-2x\leq9-5 \\ -14\leq-2x\leq4 \\ (-14)/(-2)\ge(-2x)/(-2)\ge(4)/(-2) \\ 7\ge x\ge-2 \\ -2\leq x\leq7 \end{gathered}`

Therefore, the solution is the interval [-2,7], and the graph of it would be