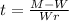Question

M=W(1+rt) (solve the following formula for "t"

Answer 1

Given the following formula given in the exercise:

`M=W\mleft(1+rt\mright)`

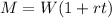
You can solve for the variable "t" by following the steps shown below:

1. You must apply the Disrtributive proprerty on the right side of the equation:

`\begin{gathered} M=(W)\mleft(1)+(W)(rt\mright) \\ M=W+Wrt \end{gathered}`

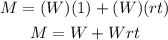
2. Now you need to apply the Subtraction property of equality by subtracting "W" from both sides of the equation:

`\begin{gathered} M-(W)=W+rtW-(W) \\ M-W=Wrt \end{gathered}`

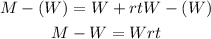
3. Finally, you can apply the Division property of equality by dividing both sides of the equation by "Wr":

`\begin{gathered} (M-W)/(Wr)=(Wrt)/(Wr) \\ \\ t=(M-W)/(Wr) \end{gathered}`

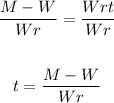
The answer is:

`t=(M-W)/(Wr)`