Using the table, we have the following points:
(x1, y1) ==> (2.5, 3), (3.5, 4.5), (5, 4.8), (5.5, 5.2), (6, 5.5)
Let's find the correlation coefficient.
To find the correlation coefficient, apply the formula:
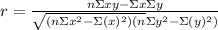
Where:
n = 5
Σx = 2.5 + 3.5 + 5 + 5.5 + 6 = 22.5
Σy = 3 + 4.5 + 4.8 + 5.2 + 5.5 = 23
Σxy = 2.5⋅3 + 3.5⋅4.5 + 5⋅4.8 + 5.5⋅5.2 + 6⋅5.5 = 108.85
Σx² = 2.5² + 3.5² + 5² + 5.5² + 6² = 109.75
Σy² = 109.6
Plug in values in the formula and solve for r.
We have:
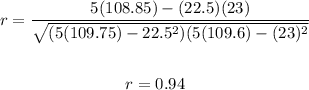
Therefore, the coefficient is 0.94
ANSWER:
0.94