Question

Use the limit definition of the derivative to find the instantaneous rate of change of

Answer 1

Step 1:

In this question, we are given the following:

Use the limit definition of the derivative to find the instantaneous rate of change of

Step 2:

The details of the solution are as follows:

An alternative way to find the use the limit definition of the derivative to find the instantaneous rate of change of:

`f(x)\text{ =}\sqrt[]{4x+8\text{ }}\text{ at x = 4}`

Let us take the derivative of the function and we have that:

`\begin{gathered} f(x)\text{ = }\sqrt[]{4x+8}=(4x+8)^{(1)/(2)} \\ \end{gathered}`
`\begin{gathered} f^I(x)\text{ = }(1)/(2)(4x+8)^{-(1)/(2)}(4) \\ f^I(x)=2(4x+8)^{-(1)/(2)},\text{ when x = 4, we have that:} \\ f^I(4)=2(4(4)+8)^{-(1)/(2)} \end{gathered}`
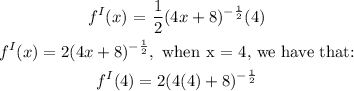
`\begin{gathered} f^I(4)=2(16+8)^{-(1)/(2)} \\ f^I(4)\text{ = 2 x }\frac{1}{\sqrt[]{24}} \end{gathered}`
`f^I(4)\text{ =}\frac{2}{\sqrt[]{24}}`
`f^I(4)=\frac{2}{\sqrt[]{24}}=\frac{2}{\sqrt[]{4}X\sqrt[]{6}}=\frac{2}{2X\sqrt[]{6}}=\frac{1}{\sqrt[]{6}}`
`f^I(4)\text{ =}\frac{1}{\sqrt[]{6}}`