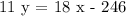SOLUTION:
Step 1:
In this question, we are given the following:
Find the equation of the line through the point (10,-6) that is perpendicular to the line with equation
-11x-18y=-2070
Step 2:
The details of the solution are as follows:
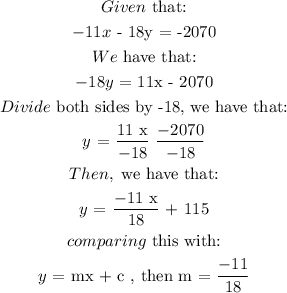

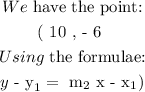
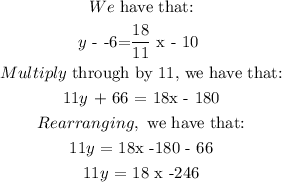
CONCLUSION:
The final answer is: