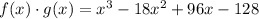Given the functions
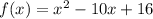
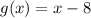
You have to calculate
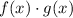
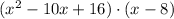
To solve this you have to apply the distributive property of multiplications, that is, you have to multiply each term of the first parenthesis with each term of the second parenthesis.
As follows:
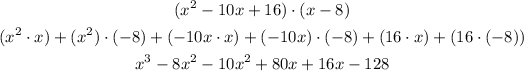
Now simplify the like terms
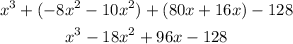
The result in standard form is