Answer:
A)
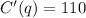
B)
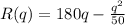
C)
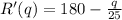
D)
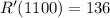
E)
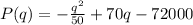
F)
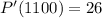
Step-by-step explanation:
Given:
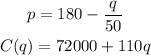
where q = the number of microwaves that can be sold at a price of p dollars per unit
C(q) = the total cost (in dollars) of producing q units.
A) To find the marginal cost, C'(q), we'll go ahead and take the derivative of the total cost as seen below;
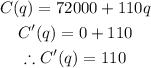
So the marginal cost, C'(q) = 110
B) We'll go ahead and determine the revenue function, R(q), by multiplying the price, p, by the quantity, q, as seen below;
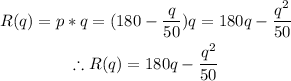
C) We'll go ahead and determine the marginal revenue function, R'(q), by taking the derivative of the revenue function, R(q);

D) To evaluate the marginal revenue function at q = 1100, all we need to do is substitute the q with 1100 in R'(q) and simplify;
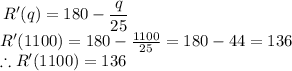
Therefore, R'(1100) is 136
E) To find the profit function, P(q), we have to subtract the total cost, C(q), from the revenue cost, R(q);
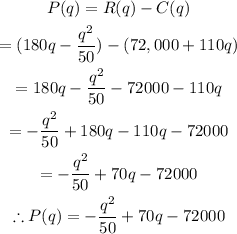
F) To Evaluate the marginal profit function at q = 1100, we have to first determine the marginal profit, P'(q), by taking the derivative of the profit function, P(x);
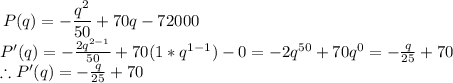
We can now go ahead and find P'(1100) as seen below;
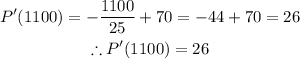
So P'(1100) = 26