The model given is:
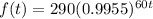
The term in the parentheses represents the change of rate of the model. If the number is the parentheses is less than 1, we call it exponential decay.
If the number in parentheses is bigger than 1, we call it exponential growth.
In this case, the correct option is "decaying"
The number in parentheses let's call it R, is:
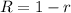
Where r is the rate of change. To find it:
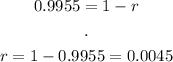
To convert to percentage, we convert by multiplying by 100::
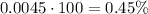
The second answer is 0.45%
And since t is the time passed in hours, and has a "60" multiplying it, the last answer is: Every 60 hours
The final answer is:
The function is exponentially decaying at a rate of 0.45% evary 60 hours.