Question

The abc one is my question could I please get sum help

Answer 1

For this problem, we are given two sides and one angle of a triangle. We need to determine the length of the side that is opposite to the known angle.

To solve this problem, we need to use the law of cosines.

`a=√(b^2+c^2-2bc\cdot\cos(m\angle A))`

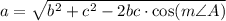
Applying the given data, we have:

`\begin{gathered} a=√(13^2+21^2-2\cdot13\cdot21\cdot\cos(105))\\ \\ a=√(169+441-546\cdot(-0.2588))\\ \\ a=√(610+141.3048)\\ \\ a=√(751.3048)=27.41 \end{gathered}`

The correct answer is 27.4.