Given the function of the rate of change of the population:
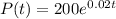
The integral of this function will be the value of the population growth of the town from 1990 to 2010. This is because P(t) is the rate of change of population, its integral will be the antiderivative, that is the population of the town.
To calculate the change in population we have to find the integral from 5 to 10 of P(t):
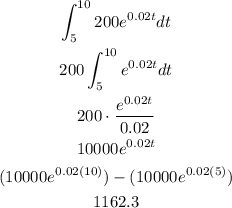
The change in population can not be a decimal number, so we can round it to 1162.
To calculate the population in 2020 we have to find the integral from 0 to 30 of P(t) and then add it to 10000 which was the initial population (we already know the integral so we're just going to evaluate it):
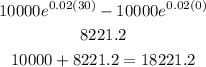
It means that the population in 2020 is 18221 (Remember that we round it because it is not possible to have a decimal value for the population of the town).