Answer:
a.
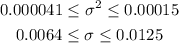
b. The standard deviation is at an acceptable level
Step-by-step explanation:
The confidence interval for the variance can be calculated as:

Where n is the size of the sample, s² is the variance of the sample, (1-∝) is the level of confidence, and χ² is the value of chi-square with n-1 degrees of freedom.
In this case, we get that n is 14 tablets, s² is 0.000071, and 1-∝ = 90%, so ∝ is 10%.
Then, the values of chi-square with 13 (14 -1) degrees of freedom is:
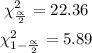
Therefore, the interval of confidence for the population variance is:
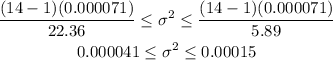
Then, the standard deviation is the square root of the variance, so the interval of confidence for the population standard deviation is:
![\begin{gathered} \sqrt[]{0.000041}\leq\sigma\leq\sqrt[]{0.00015} \\ 0.0064\leq\sigma\leq0.0125 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/356fgicskzhhlvogmsez26lb1jwuzjesk6.png)
Finally, since the upper limit of the interval for the standard deviation is less than 0.15 milligrams, we can say that the population standard deviation is at an acceptable level with a confidence level of 90%