1 Answer

Aliuk · Answer 1 · 2023-11-01T21:08:34+0000

on5x - 1 < 19

To solve this inequality add 1 to both sides

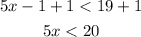
$\begin{gathered} 5x-1+1<19+1 \\ 5x<20 \end{gathered}$

Now divide both sides by 5

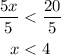
$\begin{gathered} (5x)/(5)<(20)/(5) \\ x<4 \end{gathered}$

The solutions lie in the area left to the number 4

For the second inequality

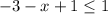
$-3-x+1\leq1$

Add first we will add the like terms in the left side

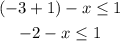
$\begin{gathered} (-3+1)-x\leq1 \\ -2-x\leq1 \end{gathered}$

Now add 2 for both sides

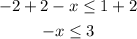
$\begin{gathered} -2+2-x\leq1+2 \\ -x\leq3 \end{gathered}$

We need to divide both sides by -1, but we should reverse the sign of inequality

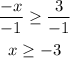
$\begin{gathered} (-x)/(-1)\ge(3)/(-1) \\ x\ge-3 \end{gathered}$

We reversed the sign of inequality when divides it by -ve number

Since 2 < 3

Then if we divide both sides by -1, then it will be

-2 < -3 which is wrong -2 greater than -3, then we should reverse the sign of inequality if we multiply or divide it by a negative number

Then the solutions of the 2nd inequality lie right to -3

Let us draw them

The red part is the solution to the 1st inequality

The blue par is the solution to the 2nd inequality

The area with the 2 colors is the area of the common solution of both inequalities

Please log in or register to add a comment.