ANSWER
4(x + 3)(x + 4)
Step-by-step explanation
We want to factorise:
4x² + 28x + 48
We simply want to write the expression as a product of its factors.
First, because each of the coefficients in the expression and the constant are divisible by 4, we will factor out 4:
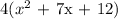
Now, we have to look for two numbers such that adding them will yield 7 and their product will yield 12.
The two numbers we need are:
3 and 4
So, we have that the expression becomes:
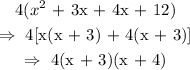
We have factorised it.