Question

A custom printing store is planning on adding painter's caps to its product line. For the first year, the fixed costs for setting up production are $10000. The variable costs for producing adozen caps are $5. The revenue on each dozen caps will be $15. Find the total profit P(x) from the production and sale of x dozen caps and the break-even point.P(x)=( ) x- ( )The break-even point is ( ),( )

Answer 1

The profit made is calculated as:

`Profit=Revenue-\text{Costs}`

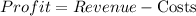
Revenue:

The revenue cost on each dozen caps is $15. If there are x dozen caps, then the revenue will be:

`Revenue=15x`

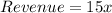
Costs:

The costs are divided into fixed cost and variable cost.

The fixed cost is $10000.

The variable cost is $5 per dozen caps. Therefore, for x dozen caps, it will be:

`\Rightarrow5x`

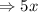
Hence, the total costs will be:

`C(x)=(10000+5x)`

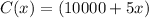
Profit Function:

Given the revenue and costs gotten, we have the profit function to be:

`\begin{gathered} P(x)=15x-(10000+5x) \\ P(x)=15x-5x-10000 \\ P(x)=10x-10000 \end{gathered}`

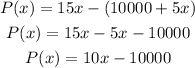
The profit function is:

`P(x)=10x-10000`

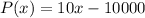
Break-even Point:

The break-even point is the point at which total revenue equals total costs or expenses.

Therefore, the break-even point will be:

`Revenue=\text{ Costs}`

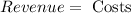
Hence,

`\begin{gathered} 15x=10000+5x \\ 15x-5x=10000 \\ (10x)/(10)=(10000)/(10) \\ x=1000 \end{gathered}`

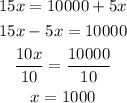
The break-even point is after the sale of 1000 dozen caps.