To check wheter a polynomial, d(x), is a factor of another, p(x), we can divide the polynomial p(x) by the d(x). If the remainder is 0, polynomial d(x) is a factor of p(x).
Since the factor we want to check is a linear polynomial, we can use synthetic division.
The polynomial is x + 4, so the number we will use as divisor is the value that makes it zero:
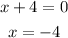
So, we put -4 in the first column:
-4 |
|
|
The rest of the first row are the coefficients of the polynomial we are dividing:
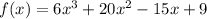
So, we have:
-4 | 6 20 -15 9
|
| 6
We also copy the first coefficient to the last row.
Now, we multiply the number on the last row of the current column by the divisor, -4. The result goes under the next coefficient:
-4 | 6 20 -15 9
| -24
| 6
Now, we add the number in the first and second rows:
-4 | 6 20 -15 9
| -24
| 6 -4
Now, we will repeat for the current column: multiply and add:
-4 | 6 20 -15 9
| -24 16
| 6 -4 1
And again:
-4 | 6 20 -15 9
| -24 16 -4
| 6 -4 1 5
Now, we will look to the last row.
The last number is the remainder, and the others are the coeficients of the quotient polynomial.
We are interested in the remainder. As said before, if the remainder is 0, x + 4 is factor, if the remainder is different than zero, x + 4 is not factor.
The remainder is:

So, since it is not zero, it is not factor of f(x).
Answer: it is not factor of f(x) and the reason is that its remainder is 5,so the best alternative is c.