Question

For the geometric sequence find the two missing clearance between 243 and -9

Answer 1

We have a Geometric Progression and this means that any term differs from its preliminary and subsequent terms by a ratio that will be represented below:

`\begin{gathered} T_n=ar^(n-1) \\ \text{where:} \\ T_n=\text{Arbitrary Term} \\ a=\text{ First term} \\ r\text{ = common ratio} \\ n=\text{ordinal of the term} \end{gathered}`

In our question, we are asked to find the 2nd term and 3rd term, we're to find T when n is 2 and 3.

First though, we need to find ratio, r

`\begin{gathered} a=243 \\ T_4=ar^3=243* r^3 \\ -9=243* r^3 \\ r^3=-(9)/(243)=-(1)/(27) \\ \text{Getting the 3rd roots of both sides gives:} \\ r=-(1)/(3) \end{gathered}`

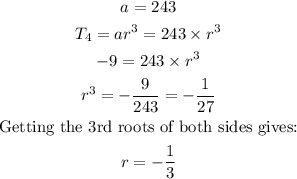
Having gotten our value of r, we proceed to find the 2nd term and 3rd terms with the formulae

`\begin{gathered} T_2=ar^(2-1)=ar \\ T_2=243*((-1)/(3))^{}=-81 \end{gathered}`
`\begin{gathered} T_3=ar^(3-1)=ar^2 \\ T_2=243*((-1)/(3))^2=27 \end{gathered}`

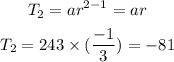
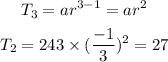
Therefore,

2nd Term = -81

3rd Term = 27