To find the derivative of the function s we can use the two following approaches:
0. Product rule.
,
1. Using trigonometric identities.
Product rule.
We know that the product rule states that:
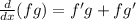
Using this rule in this case we will have:
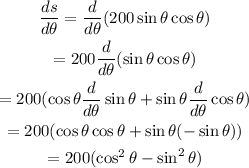
Therefore, using the product rule, we have that:
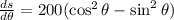
Using trigonometric identities.
We can also calculate the derivative if we remember that:
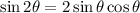
Then, in this case we have:
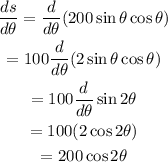
Therefore, using trigonometric identities, we have that:
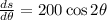
Note: Both results are equivalent, to prove it we just need to remember that:
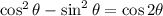
If we use this identity in the first result we get the second one.