Question

You place your holiday money in a bank that compounds interest continuously.What interest rate must the bank offer if you want to double your money in seven years?(Round to the nearest hundreth of a percent)

Answer 1

Hello! We can solve this exercise using the formula to calculate compound interest:

`A=P\cdot e^(rt)`

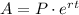
Let's suppose P = 100, so A must be approximate 200 (double).

t = 7 years

r = unknown rate

e = mathematical constant

`\begin{gathered} 200=100\cdot e^(7r) \\ \end{gathered}`

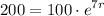
Now, let's solve it:

`\begin{gathered} 100\cdot e^(7r)=200\text{ (simplify both sides by 100)} \\ e^(7r)\text{ = 2} \\ \ln (e^(7r))=\ln (2) \\ 7r=\ln (2) \\ \\ (7r)/(7)=(\ln(2))/(7) \\ \\ r=(1)/(7)\ln (2) \end{gathered}`

Using a calculator, we have ln(2) = 0.69314718056, so we have to divide it by 7, obtaining r = 0.099.

So, the interest rate must be equal to 0.10.