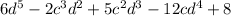We are given the result of adding two polynomials is:

One of the polynomials that is added is:

To determine the polynomial that was added we will use a polynomial with the same variables that appear on each polynomial but with unknown coefficients, like this:
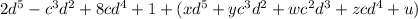
Now we associate like terms:
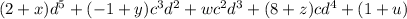
Now, each of the new coefficients must be equal to the coefficients in the resulting polynomial, therefore, we have for the first term:
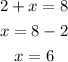
For the second term:
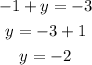
For the third term:
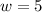
For the fourth term:
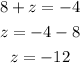
For the last term:
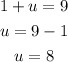
Now that we have the coefficients we can substitute in the polynomial we added, we get: