The statement is given ''A polynomial function is continuous for all real numbers" .
Consider the polynomial

Since every polynomial function is valid for every rela number.
Prove continuity for the polynomial function at any point c.
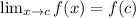
For LHS,
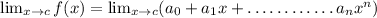
Susbtitute x=c.

For RHS

Then LHS=RHS.
The function is continuous at x=c.
Hence every polynomial function is continuous for all real numbers.
The correct option is A.