Question

In a survey, 32 people were asked how much they spent on their child's last birthday gift. The results were roughly bell-shaped with a mean of $36 and standard deviation of $6. Find the margin of error at a 99% confidence level . Give your answer to two decimal places

Answer 1

Given:

In a survey, the sample size = 32

The results were roughly bell-shaped.

The mean = μ = 36

The standard deviation = σ = 6

We will find the margin of error at a 99% confidence level.

We will use the following formula:

`e=z*(\sigma)/(√(n))`

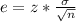
The value of the z-score that corresponds to a 99% confidence level = 2.575829

Substitute with data:

`e=2.575829*(6)/(√(32))=2.73208`

Rounding to two decimal places.

So, the answer will be:

The margin of error = 2.73