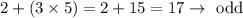Question

When an even number is added to the product of two odd numbers, the result will be even. A counterexample is 2x3+?=?

Answer 1

Consider m and n positive integers; then,

`\begin{gathered} 2m-1 \\ 2n-1 \end{gathered}`

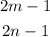
are odd numbers; thus, the product of these two is

`\begin{gathered} (2m-1)(2n-1)=4nm-2m-2n+1 \\ \Rightarrow(2m-1)(2n-1)=4mn-2(m+n)+1 \\ \Rightarrow(2m-1)(2n-1)=2(2mn-(m+n))+1 \end{gathered}`

The first term is an even number (because it is multiplied by 2). If we add +1 to an even number, the result is an odd number; therefore, the product of two odd numbers is an odd number.

Consider the following odd and even numbers,

`\begin{gathered} 2j\to\text{ even} \\ 2k-1\to\text{ odd} \\ \Rightarrow2j+(2k-1)=2(j+k)-1=2p-1\to\text{ odd number} \end{gathered}`

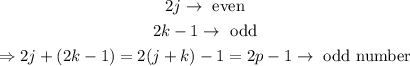
Therefore, the odd+even=odd.

The mistake in the question is that 2x3 is a product of an even number by an odd number, not a product of odd numbers.

A counterexample is

`2+(3*5)=2+15=17\to\text{ odd}`