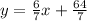SOLUTION
For a line to be perpendicular to another line, product of thier gradient must be -1.
if the gradient is given as
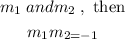
Then given the line
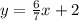
The gradient of the line is the coefficient of x using the expression
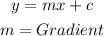
Hence, we have
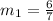
Then, using
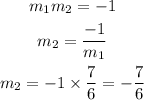
Given the point (-6,4), the line perpendicular will be having the equation
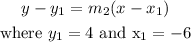
Then we obtain
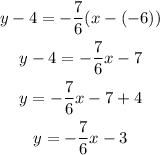
Therefore the equation perpendicular to this line is given as y=-7/6x - 3
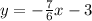
Then the equation parallel to the same line will have the same gradient
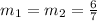
Then the equation parallel passing through the point (-6,4) will be
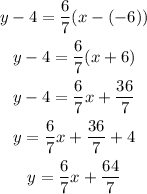
The equation of the line that is parallel to this line and passes through the point (-6, 4) will be y=6/7x+64/7