Answer:
∠RQT = 23.5
∠PQR = 133°
Explanation:
Question 1
Step 1 - Add angles together:
As all angles on a straight line must add up to 180°:
3x - 5 + x + 1 = 180
Add like terms together
3x + x - 5 + 1
4x - 4 = 180
Step 2 - Add 4 to both sides of the equation:
4x - 4 + 4 = 180 + 4
4x = 184
Step 3 - Divide both sides by 4:
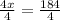
x = 46
∠RQS = x + 1
∠RQS = 46 + 1
∠RQS = 47
Given the ray QT bisects ∠RQS, the angles must be the same on either side so:
47 ÷ 2 = ∠RQT
∠RQT = 23.5
Question 2
As we know the value of x:
∠PQR = 3x - 5
Plug known values in:
3x - 5
3(46) - 5
138 - 5
∠PQR = 133°
This can also be calculated by subtracting known angle ∠RQS from 180:
180 - 47 = 133.
Hope this helps!