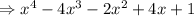Given the roots of the equation to be:
![x=-1,1,2\pm\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/u57i8iq0brjqbkqprd09s5m4u6zc8cjay8.png)
Therefore, the factors are:
![(x+1),(x-1),(x-2+\sqrt[]{5}),(x-2-\sqrt[]{5})](https://img.qammunity.org/2023/formulas/mathematics/college/ka7jh7jsm7skv1bkcy9tgdlf79d3u2qgvm.png)
To get the polynomial, we will multiply the factors together:
![\Rightarrow(x+1)(x-1)(x-2+\sqrt[]{5})(x-2-\sqrt[]{5})](https://img.qammunity.org/2023/formulas/mathematics/college/g5utl74augxv2gszuaq7k7x2l1mlyos9yo.png)
Expanding in pairs, we can have:
![\Rightarrow\lbrack(x+1)(x-1)\rbrack(x-2+\sqrt[]{5})(x-2-\sqrt[]{5})](https://img.qammunity.org/2023/formulas/mathematics/college/asxaz9i0n218t9pobsbrgxuoo1gwjqdjke.png)
Recall the Difference of Two Squares given to be:
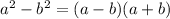
Hence, the first pair becomes:
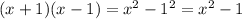
Hence, the polynomial becomes:
![\Rightarrow(x^2-1)\lbrack(x-2+\sqrt[]{5})(x-2-\sqrt[]{5})\rbrack](https://img.qammunity.org/2023/formulas/mathematics/college/p17r6e5ujnv4ovkpqwof123mcn038kwnmx.png)
Expanding the pair:
![(x-2+\sqrt[]{5})(x-2-\sqrt[]{5})=x^2-2x-x\sqrt[]{5}-2x+4+2\sqrt[]{5}+x\sqrt[]{5}-2\sqrt[]{5}-5=x^2-4x-1](https://img.qammunity.org/2023/formulas/mathematics/college/5jzsac28a6o4ixiy7040ggipinheuic49d.png)
Hence, the expression becomes:
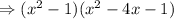
Expanding, we get:
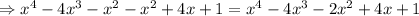
Therefore, the polynomial is: