Question 43.
Given the equation:
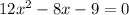
Let's solve using the quadratic formula.
Apply the quadratic formula:
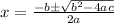
Use the standard formula to find the values of a, b and c:
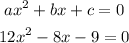
Where:
a = 12
b = -8
c = -9
Input values into the quadratic formula and solve for x:
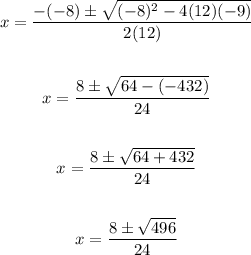
Solving further:
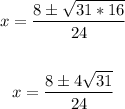
Now, let's simplify:
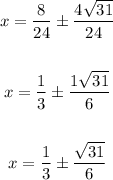
ANSWER:
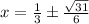
±