Question

1. Joe bought a new car in 2011 for $35,000. In 2015, Joe was offered a fair price of $15,000 forhis car, but he turned it down.a) Build a linear algebraic model, (i.e., a function), that helps Joe find the car's value when itis t years oldb) Use your model to give an estimate to the current value of Joe's car?c) When will the value of the car be $20000 dollars. (According to your model)?

Answer 1

ANSWER FOR A)

we know that the linear equation in slope intercept form is equal to

`y=mx+b`

where m is the slope of unit rate of the linear equation, b is the y-intercept or initial value of the linear equation.

Let x be the number of years since 2011 and y the car value. In this problem the year 2011 represent x = 0 so the year 2015, represent x = 4 years (2015-2011) we have the ordered pairs (x1, y1) = (0, 35,000) and (x2, y2) = (4, 15,000). With this points we are going to find the slope (m), the formula to calculate the slope between two points is equal to

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1)=(15,000-35,000)/(4-0) \\ m=(-20,000)/(4)=-5,000 \end{gathered}`

this is per year and is negative because is a decreasing function. We have when x = 0 that

`\begin{gathered} 35,000=-5,000(0)+b \\ b=35,000 \end{gathered}`

substitute the given values equation is

`y=-5,000x+35,000`

ANSWER FOR B)

If we want to know the current value of Joe's car we need to take in count the current year that is 2021 that represents x = 10 (2021 - 2011), and substitute in the equation of the point A we have that

`\begin{gathered} y=-5,000(10)+35,000 \\ y=-50,000+35,000=-15,000 \end{gathered}`

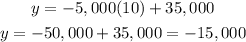
As the function is a decreasing function we have that in this year actually Joe owe money for the car. But may be this would not be the case, we need more information to give a better model that takes in count another factors, but for this model the value of Joe's car is - 15,000.

ANSWER FOR C)

To know this we need to find when y = 20,000, so we are going to substitute in the equation of the point A,

`\begin{gathered} 20,000=-5,000x+35,000 \\ 20,000-35,000=-5,000x \\ (20,000-35,000)/(-5,000)=x \\ x=(-15,000)/(-5,000)=3 \end{gathered}`

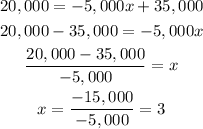
So when x=3, in the year 2014 the Joe's car is going to have a value of 20,000 dollars.