Question

In ARST, mZR = 92° and mZS = 71º. Which list has the sides of ARST in order from shortest to longest? O RS, ST, TR ORS, TR, ST O ST, RS, TR O TR, RS, ST O TR, ST, RS O ST, TR, RS

Answer 1

From the sine law we have that:

`(\sin(17))/(SR)=(\sin(71))/(RT)=(\sin (92))/(ST)`

from the first part of the equality, we obtain:

`\sin (17)RT=\sin (71)SR\Rightarrow SR=RT(\sin (17))/(\sin (71))`

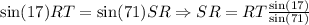
since sin(17)/sin(71) is less that 1, we conclude that RT is longer than SR

Now, comparing SR and ST with the equalities, we have that:

`\sin (17)ST=\sin (92)SR\Rightarrow SR=(\sin (17))/(\sin (92))ST`

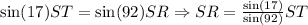
Then ST is longer than SR, now we need to compare ST AND RT

`\sin (71)ST=\sin (92)RT\Rightarrow RT=(\sin (71))/(\sin (92))ST`

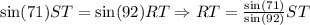
Then ST is longer Than RT, we conclude that ST is longer than RT which is longer than SR then the correct option is the SECOND ONE (RS,TR,ST)