For a principal P and a simple interest rate r for the year, the simple interest loan after a year is given by the formula:
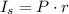
For P = $25000 and r = 9% = 0.09, we have:
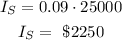
For an interest rate r' compounded quarterly, after a year the total amount would be:
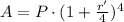
For P = $25000 and r = 8% = 0.08, we have:

Then, in this case the interest is given by:
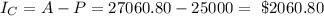
Therefore, the simple interest loan would generate 2250 - 2060.80 = $189.20 additional interest in comparisson to the retirement plan