Question

Two football players, one with a mass of 89.3 kg and the other with a mass of 94.8 kg, are running at a velocity of 8.32 m/s. If they are both headed in the same direction, what is the total momentum?

Answer 1

The momentum of first player can be given as,

`p_1=m_1v`

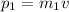
The momentum of second player can be given as,

`p_2=m_2v`

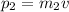
The total momentum of both the players can be given as,

`p=p_1+p_2`

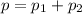
Plug in the known expressions,

`\begin{gathered} p=m_1v+m_2v \\ =(m_1+m_2)v \end{gathered}`

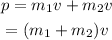
Substitute the known values,

`\begin{gathered} p=(89.3\text{ kg+94.8 kg)(8.32 m/s)} \\ =(184.1\text{ kg)(8.32 m/s)}(\frac{1\text{ N}}{1kgm/s^2}) \\ =1531.7\text{ Ns} \end{gathered}`

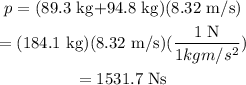
Thus, the total momentum of both the players is 1531.7 Ns.