Recall that a parabola is a curve where any point is at an equal distance from a fixed point (the focus) and a fixed straight line (the directrix).
Let (x,y) a point on the parabola with its focus at (–5,0) and its directrix y = 2, then we can set the following equation:
![\sqrt[]{(x-(-5))^2+(y-0)^2}=2-y\text{.}](https://img.qammunity.org/2023/formulas/mathematics/college/skm5i9ctrdolotcmfawoey17yp14peg9op.png)
Simplifying the above result we get:
![\sqrt[]{(x+5)^2+y^2}=2-y\text{.}](https://img.qammunity.org/2023/formulas/mathematics/college/1jf6fbrjli86qou2xwfa64vladcp1dxc2o.png)
Taking the above result to the power of 2 we get:
![\begin{gathered} \sqrt[]{(x+5)^2+y^2}^2=(2-y)^2, \\ (x+5)^2+y^2=(2-y)^2\text{.} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6c5t7r0k8zlbpdvs7exgpzdkkxs9i500uc.png)
Therefore:
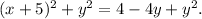
Subtracting y² from the above equation we get:
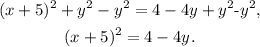
Subtracting 4 from the above equation we get:

Finally, dividing the above equation by -4 we get:
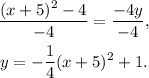
Answer: Option B.