Question

When solving square roots, when do you assign a +/- to the answer?X squared = 125

Answer 1

`\begin{gathered} x^2=125 \\ \end{gathered}`
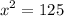
`\begin{gathered} \sqrt[]{x^2}=\sqrt[]{125} \\ \end{gathered}`

Every positive number has two square roots, one positive and one negative:

`\begin{gathered} \sqrt[]{a^2}=\pm a \\ \\ \text{Because:} \\ a\cdot a=a^2 \\ (-a)\cdot(-a)=a^2 \end{gathered}`

For solving the given expression, as 125 is not a perfect square the solution for x is both a negative and a positive:

`\begin{gathered} x=\pm\sqrt[]{125} \\ \\ x=\sqrt[]{125} \\ x=-\sqrt[]{125} \end{gathered}`

To know when do you assign a +/- to the answer you use the contex of the equation, e.g: if x is a distance it can not be negative so the solution is the positive one.

You can also simplify the square root of 125 as follow:

Prime factorization of 125:

`\begin{gathered} 125=5\cdot5\cdot5=5\cdot5^2 \\ \\ x=5(\pm\sqrt[]{5}) \end{gathered}`