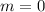The slope of a line can be calculated with the following formula:

You can notice that it is the difference between the y-coordinates and the difference between the x-coordinates of two points on that line.
For this case, knowing these points:
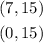
You can say that:
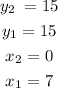
Now you can substitute values into the formula and the evaluate:
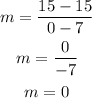
Therefore, the slope is 0: