a dilation of 2 (option A)
Step-by-step explanation:
To determine the transformation, we will use the vertices of PQRS and P'Q'R'S' and compare them
P (1, -2), Q (3, -2), R (2, -1) and S(1, -1)
P' (2, -4) Q' (6, -4), R' (4, -2) and S' (2, -2)
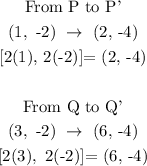
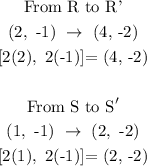
Since we multiplied the vertices of PQRS to vertices of P'Q'R'S', the transformation is a dilation of 2 (option A)