Answer:
t = 6.5
Step-by-step explanation:
Since triangle ABC and triangle XYZ are similar, the ratio of the corresponding sides is constant.
Then, AB and XY are corresponding and AC and XZ are corresponding, so
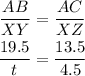
To solve for t, we need to cross multiply, so
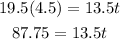
Divide both sides by 13.5
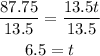
Therefore, t = 6.5