Okay, here we have this:
Considering the provided equations, that parallel lines have the same slope and the multiplication of the slopes of the perpendicular lines is -1, we are going to calculate the slope of each line, so we obtain the following:
Line 1:
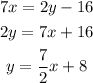
And, as the form of the equation is y=mx+b, where m is the slope, replacing in this case we obtain that the slope 7/2.
Line 2:
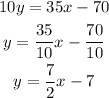
Here, we obtain that the slope is also 7/2.
Finally we obtain that the slopes are equal, so this mean that the lines are parallel.