First, we have to order the sequence:
(4,9,10,12,13,15,16,17,22)
Then we can find the mean using the following equation:
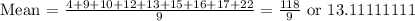
In the sequence:
(4,9,10,12,13,15,16,17,22)
The median is the number that is in the 'middle' of the sequence. In this case, it is 13.
The mode is the number that most appears. In this case, we do not have a mode because all numbers are different.
The variance can be calculated using the following equation:
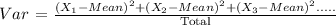
X is the element of the sequence. Total is the sequence size (9 in this case). I will do the calculations and put the result here:
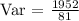
The standard deviation is calculated using the following equation:
![\text{Dev = }\sqrt[]{Var}](https://img.qammunity.org/2023/formulas/mathematics/high-school/r4m8wuch3wm37yoe4ct9e48styjjpx5o4c.png)
![\text{Dev = }\sqrt[]{(1952)/(81)=}\text{ }\frac{4\sqrt[]{122}}{9}](https://img.qammunity.org/2023/formulas/mathematics/high-school/anq95njqu5mveb3xwcpw9tk2vp0qonzn6k.png)