Question

Kevin and Joseph each decide to invest $100. Kevin decides to invest in an account that will earn $5 every month. Joseph decided to invest in an account that will earn 3% interest every month.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given Principal

`\begin{gathered} Kevin=100\text{ dollars} \\ Joseph=100\text{ dollars} \end{gathered}`

STEP 2: Determine the interests for both accounts

For Kevin

`\begin{gathered} 5\text{ dollars every month} \\ Interest\text{ in 2 months will be:} \\ 2*5=10\text{ dollars} \end{gathered}`

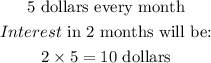
For Joseph

`\begin{gathered} 3\%\text{ of \$100 per month will be:} \\ (3)/(100)*100=3\text{ dollars per month} \\ Interest\text{ in 2 months will be:} \\ 2*3=6\text{ dollars} \end{gathered}`

STEP 3: Choose the account that will have more money in it after 2 months

`\begin{gathered} Kevin^(\prime)s\text{ account after 2 months}\Rightarrow100+10=110\text{ dollars} \\ Joseph^(\prime)s\text{ account after 2 months}\Rightarrow100+6=106\text{ dollars} \end{gathered}`

Hence, Kevin's account will have more money in it after 2 months

STEP 4: Calculate the number of months when they will have same amount of money in them

`\begin{gathered} For\text{ Kevin, the equation for amount will be:} \\ 100+5x \\ \text{For Joseph, the equation for amount will be:} \\ 100*1.03^x \\ Where\text{ x is the number of months.} \end{gathered}`

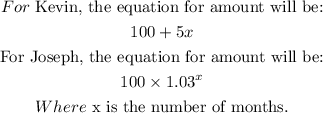
For them to have same amount, this means that:

`\begin{gathered} 100+5x=100*1.03^x \\ \text{By simplification,} \\ x=33 \end{gathered}`

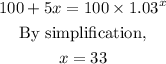
Hence, they will have same amount in the accounts after 33 months.