Question

In North America, there are three forms of currency: the Mexican peso, the Canadian dollar, and the American dollar. Although exchange rates vary, the conversion rates for these monetary systems can be modeled mathematically.In May 2007 the function A(C) = 0.911078C converted Canadian dollars, C, to American dollars, A. The function A(M) = 0.0925834M converted Mexican pesos, M, to American dollars, A.(a) Using the information that the two functions A(C) and A(M) provide, find a function to convert Mexican pesos to Canadian dollars.B) picture

Answer 1

We are required to found C(M), which is a function that converts Mexican pesos to Canadian dollars.

We can writte C(M) as C(A(M)). To do this, first let's calculate C(A), because A(C) was given, so we need to find the inverse function as follows:

`\begin{gathered} A=0.911078C \\ C=(1)/(0.911078)A \\ C=1.097600864A \end{gathered}`

Now, we have the american dollars in terms of Mexicam pesos, then let's substitute that function into the latter C(A) as follows:

`\begin{gathered} A=0.0925834M \\ C=1.097600864A \\ C=1.097600864(0.0925834M) \\ C=0.10162M \end{gathered}`

Hence, the answer to a) is C=0.10162M

Next, we have to found M(A(C)). In a similar way to the method used beforem we found that:

`M=9.84062C`

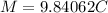
Using this equation, we replace the values of C given in the table to find the corresponding M values, the anwer b) is: 10C=98.41, 11C=108.25, 12C=118.09, 13C=127.93, 14C=137.77