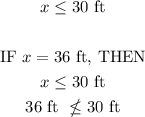Question

To be ADA compliant, wheelchair ramps require no more than a 4.8 degree slope for the ramp. How long in feet would a ramp need to be to reach a porch that is 36 inches above the ground? If ramps can be no longer than 30 feet. Can just one ramp be built to reach the porch or would a landing and another ramp be needed to stay ADA compliant? Show and explain your work using mathematical language.No picture for this problem

Answer 1

Part A:

Let x be the length of the ramp.

Drawing the diagram we have

Using the trigonometric function sine, we can solve for the length of the ramp by

`\begin{gathered} \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}} \\ \\ \text{given that} \\ \theta=4.8\degree \\ \text{opposite }=36\text{ in} \\ \text{hypotenuse }=x \\ \\ \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}} \\ \sin 4.8\degree=\frac{36\text{ in}}{x} \\ x=\frac{36\text{ in}}{\sin 4.8\degree} \\ x\approx430.2214131\text{ in} \end{gathered}`

Convert the resulting length to feet

`430.2214131\text{ in }\Longrightarrow35.851784425\text{ ft}`

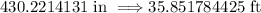
Rounding to the nearest whole number, the length of the ramp is 36 feet.

Part B:

Since the resulting ramp is greater than 30 feet, then it is not possible to build just one ramp. Given that the constraints are

`\begin{gathered} x\le30\text{ ft} \\ \\ \text{IF }x=36\text{ ft, THEN} \\ x\le30\text{ ft} \\ 36\text{ ft }\\leq30\text{ ft} \end{gathered}`