ANSWERS
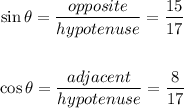
• sin(θ) = 15/17
,
• cos(θ) = 8/17
,
• sec(θ) = 17/8
Step-by-step explanation
The tangent of an angle is the ratio between its opposite side and its adjacent side,
We can use a right triangle because we know that the angle is between 0 and π/2.
If the tangent of the angle is 15/8, this means that the length of the opposite side is 15 while the length of the adjacent side is 8. Using the Pythagorean theorem, we can find the length of the hypotenuse,
![h=\sqrt[]{15^2+8^2}=17](https://img.qammunity.org/2023/formulas/mathematics/college/5kibkdpd5u1vp49s9z3t6mw77t3o7ohfkf.png)
The sine and cosine are,
The secant is the reciprocal of the cosine,
