Let x = carnations
Let y = roses
Let z = daisies
Total flowers = 200
And we have the following equations:
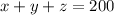
Regarding cost:
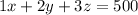
20 fewer roses than daisies is given by:
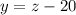
We have a system of 3 equations, so we proceed to solve:
Substitute y = z - 20
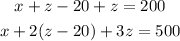
Simplify
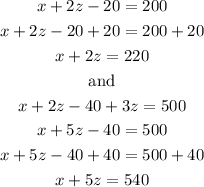
Subtract the two equations
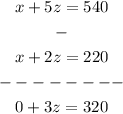
Solve for z
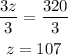
Then substitute z in y = z - 20

Next, solve for x in the first equation
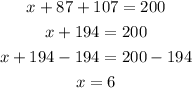
Answer:
carnations = 6
roses = 87
daisies = 107