Question

Please look at png please be as fast as possible.

Answer 1

To solve the system of equations, follow the steps below.

Step 01: Substitute y by 2x + 11 in the second equation:

`\begin{gathered} 3x+2*(2x+11)=8 \\ 3x+2*2x+2*11=8 \\ 3x+4x+22=8 \\ 7x+22=8 \end{gathered}`

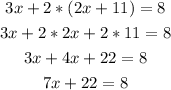
Subtract 22 from both sides:

`\begin{gathered} 7x+22-22=8-22 \\ 7x=-14 \end{gathered}`

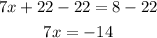
Dividing both sides by 7:

`\begin{gathered} (7x)/(7)=-(14)/(7) \\ x=-2 \end{gathered}`

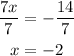
Step 02: Knowing that y = 2x + 11 , find y.

`\begin{gathered} y=2x+11 \\ y=2*(-2)+11 \\ y=-4+11 \\ y=7 \end{gathered}`

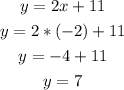
The answer of the system is (-2, 7).

Answer: y = 7.