Given two vectors A and B, we have that the expression to find their dot product is the following:
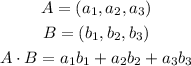
in this case, we have the following vectors:
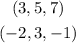
then, their dot product is:
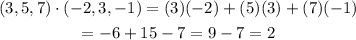
we have that the dot product between the two vectors is 2.
Since the result of the dot product is not 0, we can confirm that the two vectors (3,5,7) and (-2,3,-1) are not orthogonal