Given a triangle, with the following dimensions below
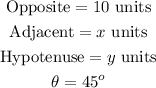
To find the value of x, we use SOHCAHTOA,
Where
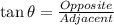
Substitute the values into the formula above
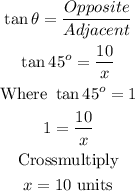
Thus, x = 10 units
To find the value of y, using the Pythagorean theorem
The Pythagorean theorem is
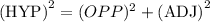
Substitute the values to find the value of y
![\begin{gathered} y^2=10^2+x^2 \\ \text{Where x}=10 \\ y^2=10^2+10^2 \\ y^2=100+100=200 \\ y^2=200 \\ \text{Square of both sides} \\ \sqrt[]{y^2}=\sqrt[]{200} \\ y=\sqrt[]{2*100}=\sqrt[]{100}*\sqrt[]{2} \\ y=10*\sqrt[]{2} \\ y=10\sqrt[]{2}\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9m78ad5n4h1zz92xktmid703rvkwdwa06r.png)
Hence, the values of x and y are
![\begin{gathered} x=10\text{ units} \\ y=10\sqrt[]{2}\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/98f60dys8fsj0s2umohyfd9jqnqrbweygc.png)