Question

how much should he charge for rent in order to bring in maximum revenue and how many units are rented then?

Answer 1

So we know that with a price of $1645 we have 111 apartments rented. We also know that for each $35 increase in rent one extra apartment remains vacant. So if the price increases to $1645+$35=$1680 there are 110 apartments rented. Let's use these two situations to build an equation. Let's use x for the rent cost per apartment and y for the number of apartments. Then we have two ordered pairs:

`\begin{gathered} (x,y)=(\text{rent cost},\text{number of apartments}) \\ (1645,111) \\ (1680,110) \end{gathered}`

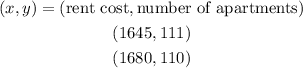
The fact that increasing the rent in $35 always leaves one extra appartment vacant means that there's a linear relation between x and y. Then we have:

`y=mx+b`

Using the two ordered pairs we can find this equation:

`\begin{gathered} (1645,111)\rightarrow y=111=m\cdot1645+b \\ (1680,110)\rightarrow y=110=m\cdot1680+b \\ 111=m\cdot1645+b \\ 110=m\cdot1680+b \end{gathered}`

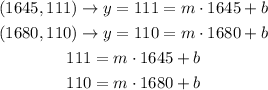
If we take the first equation and substract m*1645 at both sides we get:

`\begin{gathered} 111=m\cdot1645+b \\ 111-m\cdot1645=m\cdot1645+b-m\cdot1645 \\ 111-m\cdot1645=b \end{gathered}`

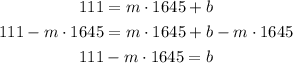
So we got an expression for b. If we replace this in the second equation:

`\begin{gathered} 110=m\cdot1680+b \\ 110=m\cdot1680+111-m\cdot1645 \\ 110-111=m\cdot(1680-1645) \\ -1=m\cdot35 \\ m=-(1)/(35) \end{gathered}`

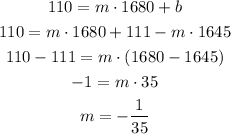
And if m=-1/35 then we get:

`\begin{gathered} b=111-m\cdot1645=111+(1645)/(35) \\ b=158 \end{gathered}`

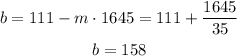
Then the equation that relates the number of rented apartments (y) and the cost of rent (x) is:

`y=-(x)/(35)+158`

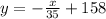
The revenue is equal to the number of rented apartments (y) multiplied by the cost of rent (x) then the revenue is given by:

`\begin{gathered} \text{revenue}=x\cdot y=x\cdot(-(x)/(35)+158) \\ \text{revenue}=-(x^2)/(35)+158x \end{gathered}`

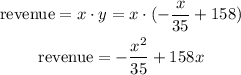
So the maximum revenue is achieved when this quadratic function is maximum. The maximum of a quadratic function is located in the midpoint between its zeros. So we first need to find the two zeros, then the x value in the middle of those two is the cost of rent that has the maximum revenue. Using the linear equation from before we can find the number of rented apartments for that value.

So first let's find the zeros of the quadratic function i.e. the x values for which the function is 0:

`-(x^2)/(35)+158x=x\cdot(-(x)/(35)+158)=0`

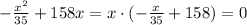
This happens when either x=0 or (-x/35+158)=0. Then we have:

`\begin{gathered} x=0 \\ -(x)/(35)+158=0 \\ -(x)/(35)=-158 \\ x=-158\cdot(-35) \\ x=5530 \end{gathered}`

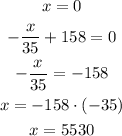
So the zeros are x=0 and x=5530. The mid-value between them is:

`(5530+0)/(2)=2765`

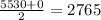
As we said this is the rent cost that has the maximum revenue. We can use it to find the number of apartments rented:

`y=-(x)/(35)+158=-(2765)/(35)+158=79`

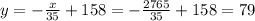
Then the answers are: $2765 per month and 79 units rented.