Question

A. A manufacturer knows that their items have a normally distributed lifespan, with a mean of 2.9 years, and standard deviation of 0.9 years.If you randomly purchase one item, what is the probability it will last longer than 5 years?B. A particular fruit's weights are normally distributed, with a mean of 450 grams and a standard deviation of 35 grams.If you pick one fruit at random, what is the probability that it will weigh between 352 grams and 470 gramsC.A particular fruit's weights are normally distributed, with a mean of 560 grams and a standard deviation of 13 grams.The heaviest 9% of fruits weigh more than how many grams?Give your answer to the nearest gram.D. The mean daily production of a herd of cows is assumed to be normally distributed with a mean of 33 liters, and standard deviation of 2.8 liters. What is the probability that daily production is less than 34.7 liters?What is the probability that daily production is more than 28.3 liters?Warning: Do not use the Z Normal Tables...they may not be accurate enough since WAMAP may look for more accuracy than comes from the table.round to 4 decimal places.

Answer 1

A. We have a normally distribute random variable with mean of 2.9 years and standard deviation of 0.9 years.

We have to find the probability that a random selected individual of this population will last longer than 5 years.

To find this we calculate the z-score for X = 5 and then calculate the probability.

We can calculate the z-score as:

`z=(X-\mu)/(\sigma)=(5-2.9)/(0.9)=(2.1)/(0.9)=2.3333`

We can now use this z-score and calculate the probability from the standard normal distribution:

`P(X>5)=P(z>2.3333)=0.0098`

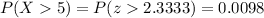
Answer: the probability that a random selected item last longer than 5 years is 0.0098.

B. In this case, the random variable is normal and has a mean of 450 g and a standard deviation of 35 g,

We have to find the the probability that the random selected fruit will weigh between 352 grams and 470 grams.

We now calculate the z-score for both limits of the interval:

`\begin{gathered} z_1=(X_1-\mu)/(\sigma)=(352-450)/(35)=(-98)/(35)=-2.8 \\ z_2=(X_2-\mu)/(\sigma)=(470-450)/(35)=(20)/(35)=0.5714 \end{gathered}`

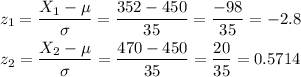
Now, we can calculate the probability that is within this interval as:

Then, knowing the z-score for which only 9% of the data is greater than it, we can convert it to our distribution:

`\begin{gathered} X=\mu+z\cdot\sigma \\ X=560+1.34076\cdot13 \\ X=560+17.42988 \\ X=577.42988 \\ X\approx577 \end{gathered}`

Answer: Approximately 9% of the fruit will weight more than 577 grams.

D. We have this random normal variable (daily production of milk per cow) with mean of 33 L and standard deviation of 2.8 L.

We have to find the probability that the production is less than 34.7 L.

We start by calculating the z-score:

`z=(X-\mu)/(\sigma)=(34.7-33)/(2.8)=(1.7)/(2.8)=0.6071`

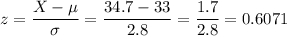
Then, we use an app or calculator to calculate the probability:

`P\mleft(X<34.7\mright)=P\mleft(z<0.6071\mright)=0.7281`

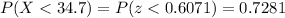
To calculate the probability that the production is more than 28.3 L, we have to proceed similarly:

`z=(X-\mu)/(\sigma)=(28.3-33)/(2.8)=(-4.7)/(2.8)=-1.6786`
`P\mleft(X>28.3\mright)=P\mleft(z>-1.6786\mright)=0.9534`

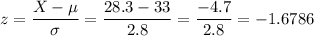
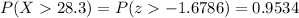
Answer:

The probability that the production is less than 34.7 L is 0.7281.

The probability that the production is more than 28.3 L is 0.9534.