Step-by-step explanation:
A perfect square trinomial has this form:

In words, a binomial squared is the first term squared plus (or minus depending on the sign into the binomial) twice the first term times the second term, plus the second term squared.
In this problem we have a part of the perfect trinomial: x²-14x
We can see that the first term of the binomial has to be x. Since the second term of the trinomial is twice the first term times the second term of the binomial:
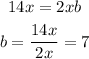
The second term of the binomial is 7:
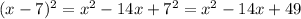
Answer:
The constant to be added is B. 49